A radical expression is composed of three parts:
a radical symbol, y radicando, Y un índice
In this tutorial, the primary focus is on simplifying radical expressions with an index of 2. This type of radical is commonly known as the square root.
Components of a Radical Expression
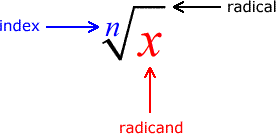
Starting with a single radical expression, we want to break it down into pieces of “smaller” radical expressions. We hope that some of those pieces can be further simplified because the radicands (stuff inside the symbol) are perfect squares. Remember, the square root of perfect squares comes out very nicely!
We need to recognize how a perfect square number or expression may look like. Let’s do that by going over concrete examples.
Examples of Perfect Squares
What makes them perfect squares?
Notice that the square root of each number above yields a whole number answer. Think of them as perfectly well-behaved numbers.
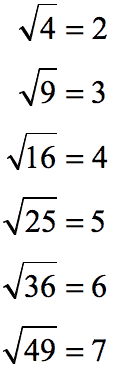
In addition, those numbers are perfect squares because they all can be expressed as exponential numbers with even powers. The powers don’t need to be “2” all the time. As long as the powers are even numbers such 2, 4, 6, 8, etc, they are considered to be perfect squares. One way to think about it, a pair of any number is a perfect square!
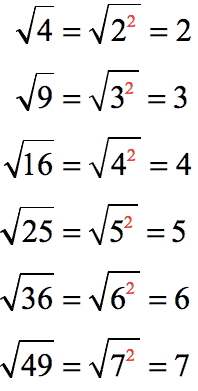
More so, the variable expressions above are also perfect squares because all variables have even exponents or powers.
Examples of How to Simplify Radical Expressions
Ejemplo 1: Simplify the radical expression sqrt {16} .
This is an easy one! The number 16 is obviously a perfect square because I can find a whole number that when multiplied by itself gives the target number. It must be 4 since (4)(4) = 42 = 16. Thus, the answer is
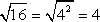
Below is a screenshot of the answer from the calculator which verifies our answer.

Ejemplo 2: Simplify the radical expression sqrt {60}.
You can do some trial and error to find a number when squared gives 60. Going through some of the squares of the natural numbers…

The answer must be some number n found between 7 and 8. So we expect that the square root of 60 must contain decimal values. To simplify this radical number, try factoring it out such that one of the factors is a perfect square. By quick inspection, the number 4 is a perfect square that can divide 60.
So our answer is…
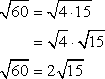
And for our calculator check…

What rule did I use to break them as a product of square roots? Here it is!
Remember the rule below as you will use this over and over again.
PRODUCT RULE OF SQUARE ROOTS
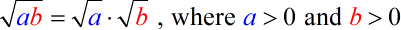
- This means that the square root of the product of a y b is equal to the product of their individual square roots.
Ejemplo 3: Simplify the radical expression sqrt {72} .
Always look for a perfect square factor of the radicand. After doing some trial and error, I found out that any of the perfect squares 4, 9 and 36 can divide 72. So which one should I pick? Actually, any of the three perfect square factors should work. However, the best option is the largest possible one because this greatly reduces the number of steps in the solution.
Compare what happens if I simplify the radical expression using each of the three possible perfect square factors. Picking the largest one makes the solution very short and to the point.
- Comience con 4
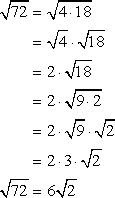
- Comience con 9
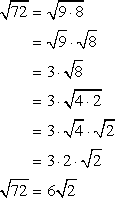
- Comience con 36
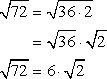
It’s okay if ever you start with the smaller perfect square factors. You just need to make sure that you further simplify the leftover radicand (stuff inside the radical symbol). Repeat the process until such time when the radicand no longer has a perfect square factor.
Looks like the calculator agrees with our answer. Great!

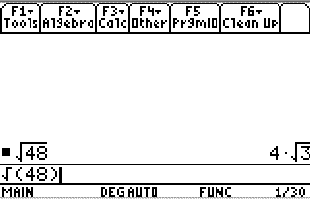
Ejemplo 4: Simplify the radical expression sqrt {48} .
Another way to solve this is to perform prime factorization on the radicand. Then express the prime numbers in pairs as much as possible. The paired prime numbers will get out of the square root symbol, while the single prime will stay inside.
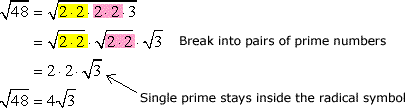
And it checks when solved in the calculator.
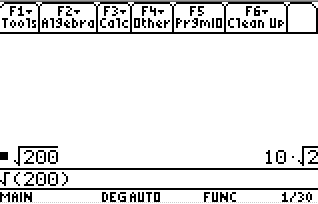
Ejemplo 5: Simplify the radical expression sqrt {200} .
Let’s find a perfect square factor for the radicand. Although 25 can divide 200, the largest one is 100. Next, express the radicand as products of square roots, and simplify.
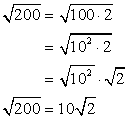
The calculator gives us the same result!
Ejemplo 6: Simplify the radical expression sqrt {180} .
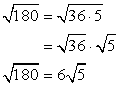
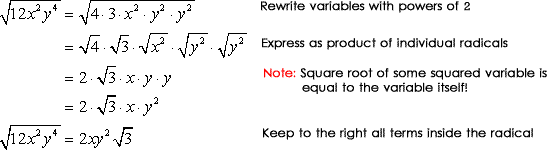
Ejemplo 7: Simplify the radical expression sqrt {12{x^2}{y^4}} .
The radicand contains both numbers and variables. Let’s deal with them separately.
For the numerical term 12, its largest perfect square factor is 4. Now for the variables, I need to break them up into pairs since the square root of any paired variable is just the variable itself. The solution to this problem should look something like this…
The standard way of writing the final answer is to place all the terms (both numbers and variables) that are outside the radical symbol delante of the terms that remain inside.
For our calculator check…
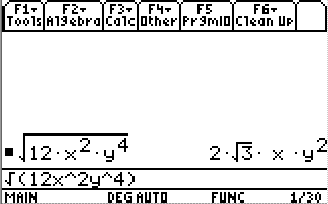
The calculator presents the answer a little bit different. However, I hope you can see that by doing some rearrangement to the terms that it matches with our final answer. Fantastic!
Ejemplo 8: Simplify the radical expression sqrt {54{a^{10}}{b^{16}}{c^7}}.
For this problem, we are going to solve it in two ways. The goal is to show that there is an easier way to approach it especially when the exponents of the variables are getting larger.
Método de emparejamiento: This is the usual way where we group the variables into two and then apply the square root operation to take the variable outside the radical symbol. You will see that for bigger powers, this method can be tedious and time-consuming.
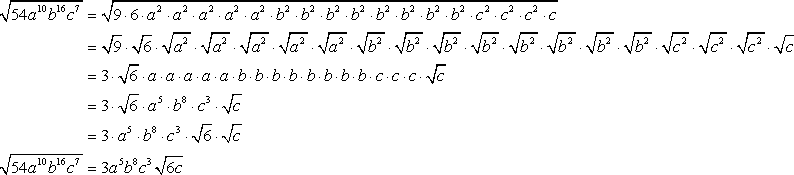
“Division of Even Powers” Method: You can’t find this name in any algebra textbook because I made it up. However, the key concept is there. The main approach is to express each variable as a product of terms with even and odd exponents. If the term has an even power already, then you have nothing to do. Otherwise, you need to express it as some even power plus 1.
Remember that getting the square root of “something” is equivalent to raising that “something” to a fractional exponent of {1 over 2}.
Simply put, divide the exponent of that “something” by 2.
- That’s the reason why we want to express them with even powers since cualquier even number is divisible by 2.

Ejemplo 9: Simplify the radical expression sqrt {400{h^3}{k^9}{m^7}{n^{13}}} .
Let’s simplify this expression by first rewriting the odd exponents as powers of an even number plus 1.
For the number in the radicand, I see that 400 = 202.
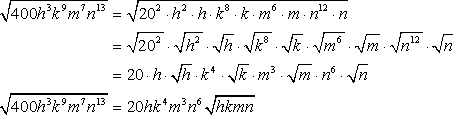
Ejemplo 10: Simplify the radical expression sqrt {147{w^6}{q^7}{r^{27}}}.
Express the odd powers as even numbers plus 1 then apply the square root to simplify further.
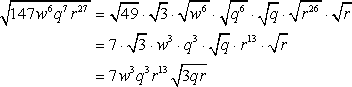
Ejemplo 11: Simplify the radical expression sqrt {32} .
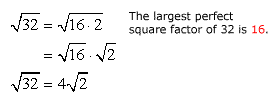
Ejemplo 12: Simplify the radical expression sqrt {125} .
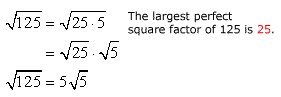
Ejemplo 13: Simplify the radical expression sqrt {80{x^3}y,{z^5}}.
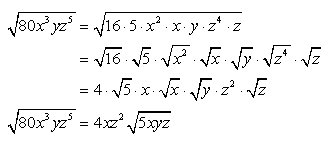
Ejemplo 14: Simplify the radical expression sqrt {18m{}^{11}{n^{12}}{k^{13}}}.
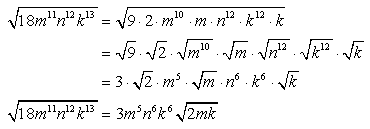
Practica con hojas de trabajo
Te podría interesar:
Resolver ecuaciones radicales
Sumar y restar expresiones radicales
Multiplicar expresiones radicales
Racionalizar el denominador